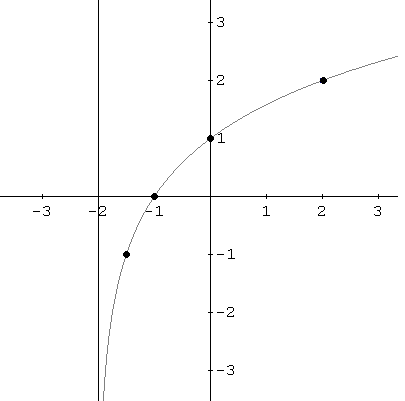Dado un número
real mayor que cero (argumento x), la función logaritmo le asigna el
exponente n (o potencia) a la que un número fijo b (base) se debe
elevar para obtener dicho argumento. Es la función inversa de
b a la potencia n. Esta función se escribe como: n = logb
x, lo que permite obtener n.
·
(se lee como:
logaritmo en base b de x es igual a n; si y sólo si b
elevado a la n da por resultado x)
El dominio de las funciones logarítmicas es (0, + ∞).
La imagen es R.
(Para que la
definición sea válida, no todas las bases y números son posibles. La base b
tiene que ser positiva y distinta de 1, luego b> 0 y b ≠ 1, x
tiene que ser un número positivo x > 0 y n puede ser cualquier
número real)
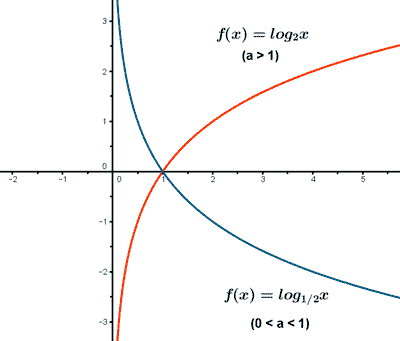
Depende del valor de b, si la función crece o decrece
·
Si b > 1 la función es
creciente
·
Si 0 < b<
1 la función es decreciente
Veamos
un ejemplo